Ring hierarchy for distributed data storage : the HARP

The goal

Repartition algorithms have one goal: spliting data or calculations as evenly as possible.

This is of course, done to match the available resources in either memory or treatment power.

State of the art

CRUSH, the distribution layout of Ceph

The distribution of data in Ceph is based on the idea of placement groups. We create a number of placement groups. Then the CRUSH algorithm assign placement groups to each server, data is replicated among the same placement group between multiple servers.

This leads, in my opinion, to some issues:

• determination of the number of placement groups.
• having to migrate the pool of data given changes in the cluster layout to please the placement group system.

The (approximate) maths behind the idea

The idea is based upon the splitting of a wide ring of integers among a comparably small number of instances.

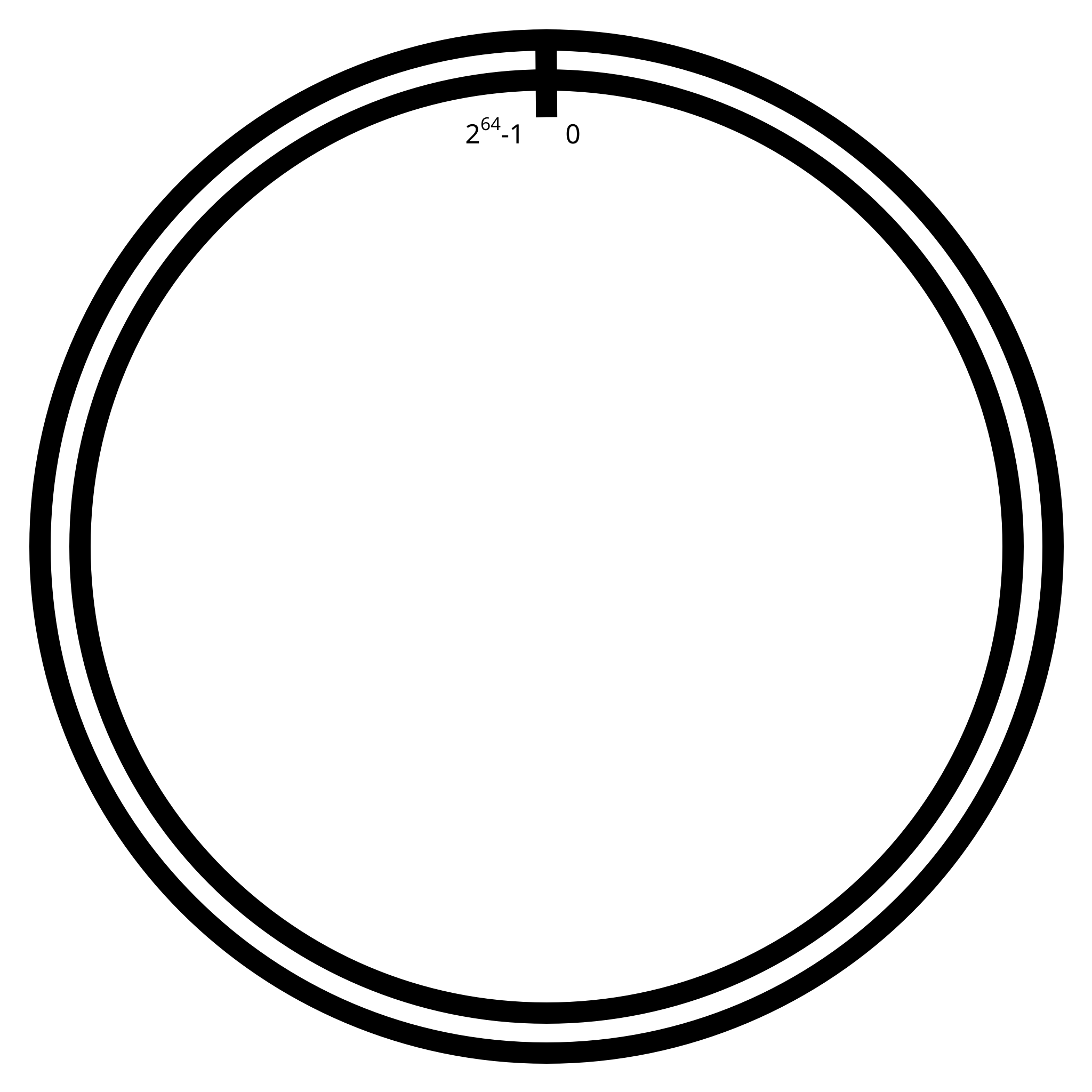
As for practical purposes, the ring of unsigned integers between 0 and 264 excluded was chosen.

The rings are considered a suite of rings, each being recording a new state of the whole cluster.

Let R(n) be a suite of rings of the natural integers in the range Rset=[0,264)

For any number n of 64 digits in base 2, this number n ∈ Rset.

Addition should wrap around the ring like a modulus addition. Which is the behavior of C-style unsigned integers.

For any number of R(n) of any n, let + in R(n) be the operator on a ∈ R(n) and b ∈ ℕ such as a+b is the lowest value r ∈ ℕ such as a+b≡r(mod 264).

As such, it is possible to get slices with a fixed distance to another by a simple addition of that distance.

It is worth noting that the ring doesn't possess subtraction or negative numbers, as such, distance is oriented and only defined by addition.

We them assign access points to daemons to slices of the ring. For this we use a ponderated value between a splitting ratio and the weight, for the next examples, only the weight will be demonstrated, making the splitting ratio be of 0.

Let R(0) a ring R(n) containing a daemon red of weight 2.

This makes us a single slice, whose boundaries are the whole ring, and whose distance between boundaries is 264-1. Since there is a single slice, the weight of 2 have no influence here for now.

Let Sred be a slice of this ring representing all of the ring. This slice is named, the slice of R(0) assigned to the daemon red.

Now what about when we add a new daemon to the chain of rings?

Let be R(1) a ring R(n), this ring being equal to R(0) with the addition of a daemon green of weight 1.

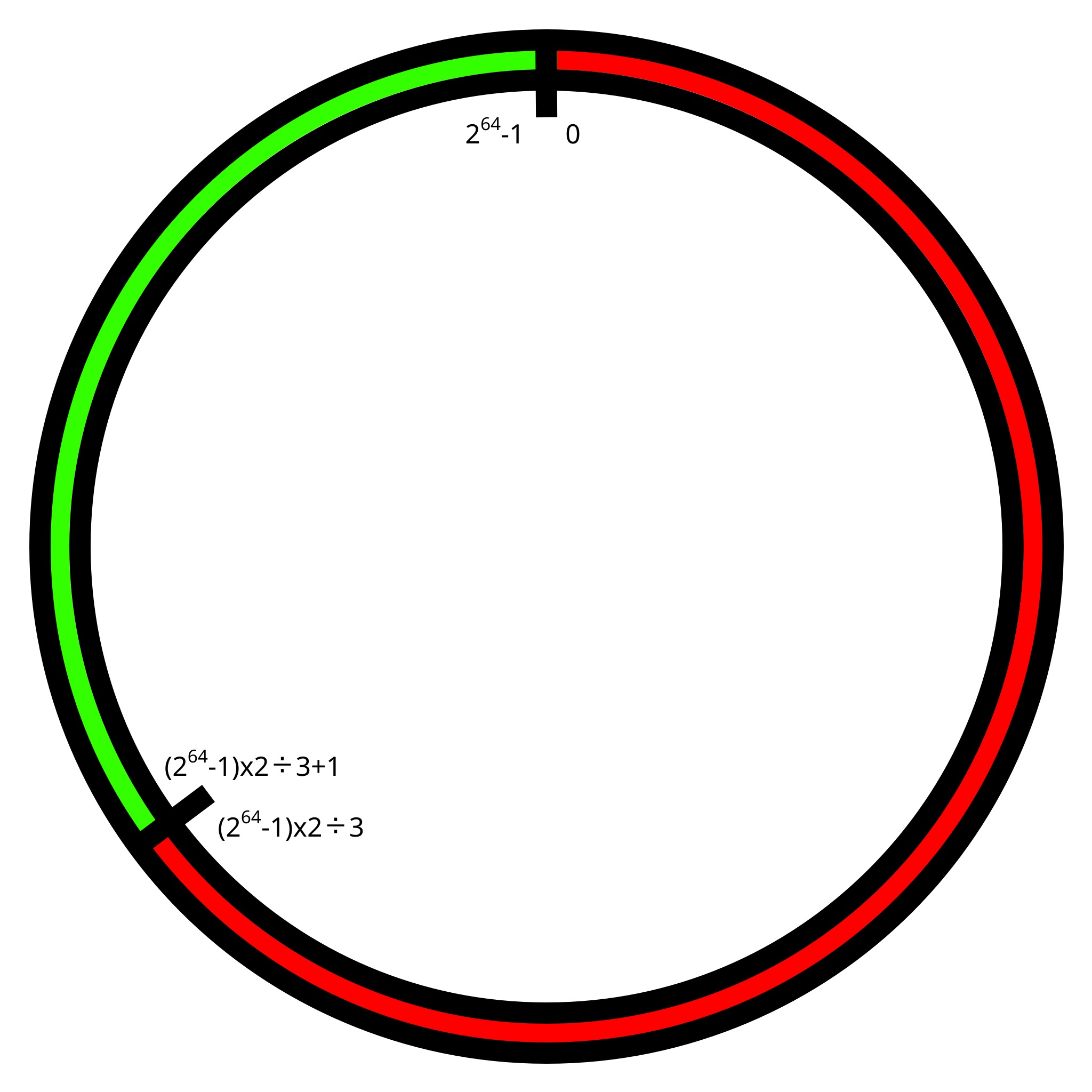
When adding another ring to the set, with here a weight of 1, the slices will be split among the 2, with 2/3 rounded down to the daemon with weight 2, and the rest to the other.

Let Sred be a slice of this ring representing two thirds of the values in ring starting at 0 and increasing up to (264-1)×2÷3. This slice is named, the slice of R(1) assigned to the daemon red.

Let Sgreen be a slice of this ring representing one thirds of the values in ring starting at (264-1)×2÷3 excluded and increasing up to 264-1. This slice is named, the slice of R(1) assigned to the daemon green.

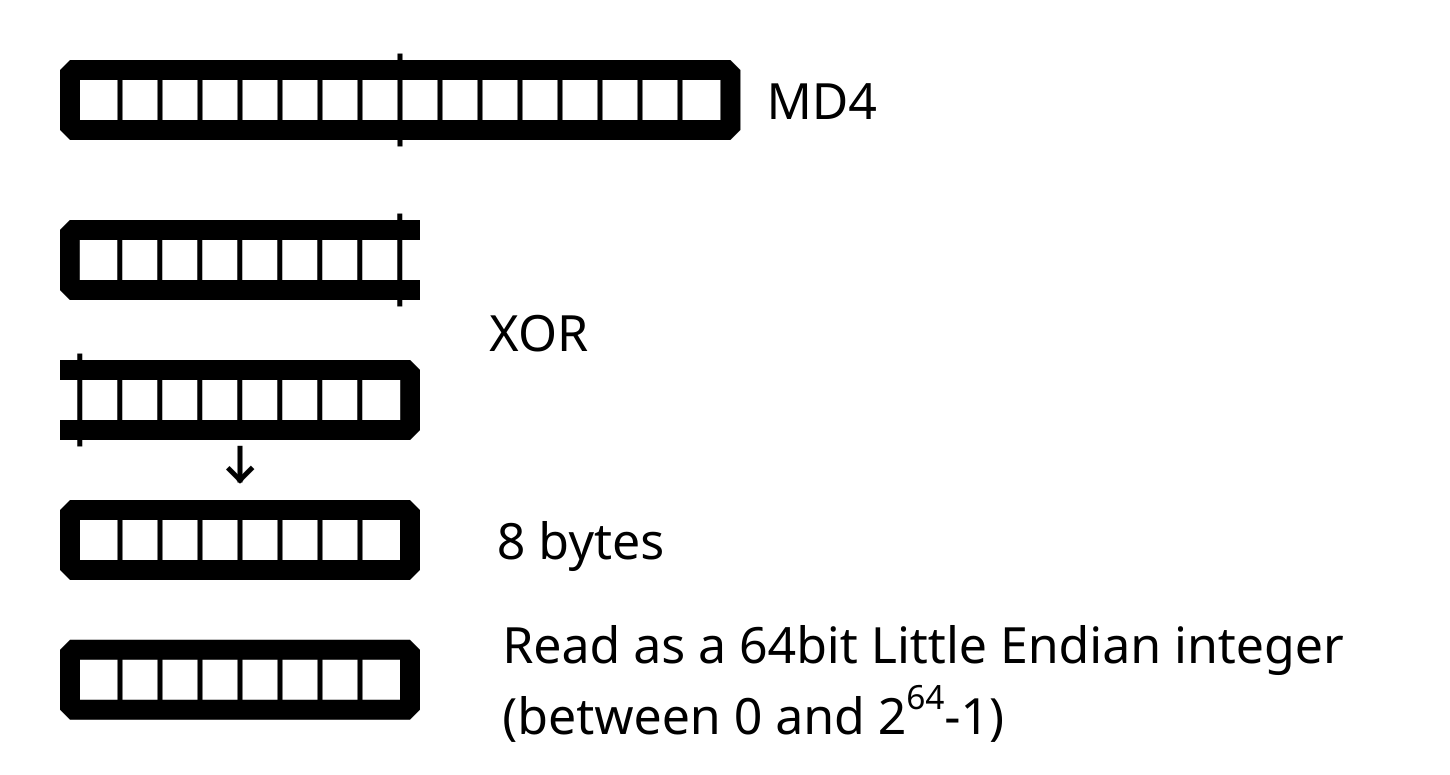
Let Tmd4 be the transform of a natural number expressed as a number of digits in base 2 that is multiple of 8 into a natural number of 128 digits in base 2 as defined by RFC 1320.

Let Thash be the transform a number of digits in base 2 that is multiple of 8 into a natural number of 128 digits in base 2 x in the following way:

• Let ahead be the number formed by the first 64 digits of Tmd4(x) and atail be the number formed by the last 64 digits of Tmd4(x).
• Thash(x) is equal to the digit by digit exclusive or of ahead and atail.

The implementation in Crystal

class Daemon
    getter weight : UInt64
    getter location : Array(Int32)
    getter url : String
    def initialize(@weight : UInt64, @location : Array(Int32), @url : String)
    end
end

class SliceInfo
    JSON.mapping(
        slices: Array(Array(Slice)),
        last: Int32,
        shards: UInt32
    )

    def initialize(@slices, @last, @shards)
    end
end

private def hash_impl(data : String)
    ctx = OpenSSL::Digest.new("md4")
    ctx << data
    digest = ctx.digest
    tag = IO::ByteFormat::BigEndian.decode(UInt64, digest)
    tag ^= IO::ByteFormat::BigEndian.decode(UInt64, digest+8)
    return tag
end

High Availability Ring Protocol

A HARP system is composed of an heterogeneous number of nodes aware of their physical placement in the cluster, as well as a number of monitors connecting them. The monitors can fully access each other and are connected over the internet.

All of the nodes and monitors being aware of the layout of the monitor ring, may a connection be severed, new connections can be made easily.

Services are to implement query interfaces as well as relocation interfaces.

Relocation occur when a node is added or removed, it is done by querying the former owners for keys within a given slice.

Results

The HARP protocol is a candidate for the implementation of the Scroda distributed currency system.

The concept of ring sets is plenty expanded within the Scroda database technical specification.

Conclusion

The concept of ring sets that govern the principles of HARP is very reusable. It provides a way to deterministically split data and treatment in a great number of servers or more generally of entities.

I invite you to check the information at https://nekoit.xyz/, join us on Discord or Telegram, or follow me on Mastodon [email protected] to receive notifications of my followup posts.